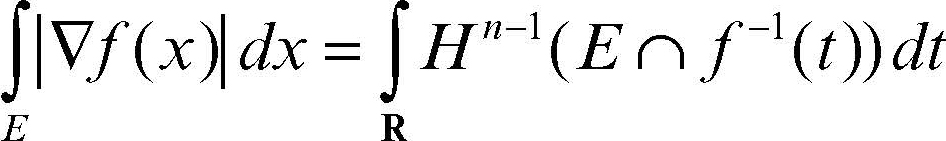Formula di coarea

In matematica, più precisamente nell'ambito della teoria della misura, la formula di coarea permette di calcolare l'integrale del gradiente di una funzione in termini dell'integrale dei suoi insiemi di livello. Tale formula viene spesso utilizzata per problemi isoperimetrici.

Enunciato

È possibile enunciare due versioni per la formula di coarea.

Prima versione

Indicando con ${\displaystyle {\mathcal {H}}^{n-1}}$ la misura di Hausdorff (n-1)-dimensionale allora, se ${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ è una funzione lipschitziana e ${\displaystyle E}$ un insieme misurabile, vale la formula:

${\displaystyle \int _{E}|\nabla f(x)|dx=\int _{\mathbb {R} }{\mathcal {H}}^{n-1}(E\cap f^{-1}(t))dt}$

Seconda versione

È possibile dare un'altra versione della formula di coarea, nella quale al primo membro compare anche un'altra funzione ${\displaystyle g}$ non negativa e misurabile. Sia ${\displaystyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ Lipschitziana e sia ${\displaystyle E}$ un insieme misurabile. Sia inoltre ${\displaystyle g:\mathbb {R} ^{n}\rightarrow [0, \infty ]}$ una funzione misurabile. Allora vale la formula:

${\displaystyle \int _{E}g(x)|\nabla f(x)|dx=\int _{\mathbb {R} }\left(\int _{E\cap f^{-1}(t)}g(y)d{\mathcal {H}}^{n-1}\right)dt}$

Applicazioni

Spesso la formula di coarea viene utilizzata nella sua seconda versione per il calcolo di un integrale di una funzione a simmetria radiale. Infatti, per calcolare l'integrale di ${\displaystyle g}$, scegliendo ${\displaystyle f=|x|}$ si ottiene:

${\displaystyle \int _{E}g(x)dx=\int _{\mathbb {R} }\left(\int _{E\cap \partial B_{r}}g(y)d{\mathcal {H}}^{n-1}\right)dr}$

dove ${\textstyle \partial B_{r}}$ è il bordo della palla ${\displaystyle n}$-dimensionale centrata nell'origine di raggio ${\displaystyle r}$.

Viene anche utilizzata per dimostrare la disuguaglianza di Pólya-Szegő.

Bibliografia

• (EN) Ambrosio, Fusco, Pallara, Function of Bounded Variation and Free Discontinuity Problems, Oxford University Press, 2000.
• (EN) Fleming, WH; Rishel, R (1960), "An integral formula for the total gradient variation", Archiv der Mathematik 11 (1): 218–222, doi:10.1007/BF01236935
• (EN) Malý, J; Swanson, D; Ziemer, W (2002), "The co-area formula for Sobolev mappings", Transactions of the American Mathematical Society 355 (2): 477–492, doi:10.1090/S0002-9947-02-03091-X.

Voci correlate

• Gradiente
• Insieme di livello
• Teorema di Brothers-Ziemer